Teorema do Posto-Nulidade, posto linha = posto coluna, etc

Alberto Saa

Abaixo vai, de uma maneira um pouco mais caprichada, o esquema da aula de hoje.

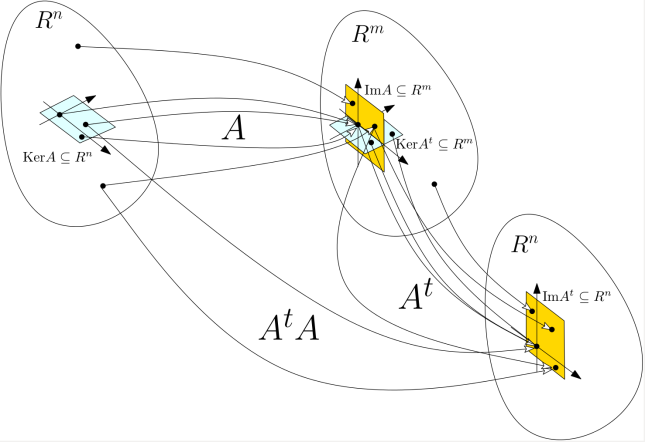
screenshot-from-2016-09-21-075240

Relembrando, estamos interpretando uma matriz A de m linhas e n colunas como uma transformação linear A:\mathbb{R}^n\to \mathbb{R}^m. Não precisamos supor nada sobre a matriz além de ser m\times n, e concluímos muitas coisas interessantes. Repetir todos os passos abaixo é um ótimo exercício.

1) Os espaços vetoriais {\rm Ker} A\subseteq\mathbb{R}^n e {\rm Im}A\subseteq\mathbb{R}^m e o Teorema Posto-Nulidade

São definidos como

{\rm Ker} A = \{ X\in \mathbb{R}^n | AX=0\}

{\rm Im } A = \{ Y\in \mathbb{R}^m | \exists X\in \mathbb{R}^n,  AX=Y\}

As dimensões destes espaços vetoriais (provem que são!) têm nomes especiais: nulidade e posto (nullity e rank), respectivamente:

{\rm null} A = {\rm dim\, Ker} A \le n

{\rm posto} A = {\rm dim\, Im} A \le m

Estas duas quantidades são relacionadas pelo chamado Teorema do Posto-Nulidade:

{\rm null} A + {\rm posto} A = n

A prova envolvia uma escolha de base para \mathbb{R}^n “adaptada” para  o subespaço {\rm Ker} A\subseteq\mathbb{R}^n, i.e.,  uma base tal que os k primeiros vetores (k ={\rm null} A  \le n) geram {\rm Ker} A e o restante (n-k vetores) cobre o complementar:

 \mathbb{R}^n = {\rm span} \{v_1,v_2,\dots,v_k,w_1,w_2,\dots,w_{n-k}\}

con

{\rm Ker} A = {\rm span} \{v_1,v_2,\dots,v_k \}

A prova envolvia basicamente mostrar que Aw_1, Aw_2,\dots eram uma base para {\rm Im} A\subseteq\mathbb{R}^m. Refaçam!

2) Posto linha = Posto coluna

Vimos que podemos aprender um pouco mais se explorarmos a transformação linear associada à matriz transposta: A^t:\mathbb{R}^m\to \mathbb{R}^n. Tudo que fizemos acima pode ser refeito aqui. A novidade é que podemos agora “compor” as transformações (veja a figura), e considerarmos também a transformação linear A^tA:\mathbb{R}^n\to \mathbb{R}^n.

O resultado fundamental era que {\rm Ker}A^tA ={\rm Ker}A (reproduzam!), o que via o Teorema Posto-Nulidade nos dá  {\rm posto} A^tA = {\rm posto} A.

Da figura, temos claramente que {\rm Im}A^tA \subseteq {\rm Im}A^t, e portanto

 {\rm posto} A = {\rm posto} A^tA \le {\rm posto} A^t

Bem, aqui o argumento é que poderíamos repetir toda a construção, mas olhando agora para a composição AA^t (façam!). Com isso, obteríamos essencialmente  {\rm posto} A^t  \le {\rm posto} A, o que nos leva ao resultado festejado

{\rm posto} A = {\rm posto} A^t,

i.e., o número de colunas LI de uma matriz é igual ao número de suas linhas LI!

Tínhamos também um resultado intermediário curioso:

{\rm Ker}A^t\cap {\rm Im}A = \{0\}

Elaborem um pouco mais e convençam-se que

\mathbb{R}^m ={\rm Ker}A^t\oplus {\rm Im}A

(\oplus = soma direta de espaços vetoriais, veja definição 3.4.2 do Pulino.)

Tudo isto é fortemente influenciado, pra não chamar de “cópia deslavada”, deste excelente artigo da nossa querida American Mathematical Monthly. Divirtam-se! O autor, Gilbert Strang, tem (ou tinha) um fantástico curso on-line de Álgebra Linear (do MIT). Seus livros do assunto também são muito bons.

IMPORTANTÍSSIMO. Hoje, na aula, dei uma informação incorreta. Disse que este material não fazia parte do conteúdo da P1, e FAZ! Confiram na ementa oficial os exercícios correspondentes do livro do Pulino para a P1.

3 comentários sobre “Teorema do Posto-Nulidade, posto linha = posto coluna, etc”

  1. Há um outro Alberto no IMECC, com igual bom gosto matemático e futebolístico, quem me alertou que o esquema dos subespaços vetorias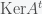 {\rm Ker}A^t e {\rm Im}A no esquema do post pode levar a confusão, pois parece que sua intersecção seria uma linha reta e não um ponto. Uma representação mais fiel seria como a da figura abaixo.

    KernTransp

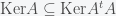    Sobre a prova de que {\rm Ker}A^tA = {\rm Ker}A, vejam primeiro que a inclusão {\rm Ker}A \subseteq {\rm Ker}A^tA é direta. Para mostrar que também temos 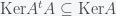{\rm Ker}A^tA \subseteq {\rm Ker}A, considerem

    A^tAX = 0 \Rightarrow X^tA^tAX = (AX)^tAX = 0

    mas a última igualdade implica que AX = 0, certo? 🙂 Veremos em breve que essa construção está relacionada à ideia de norma de vetores…

    Curtir

    Responder

Deixe um comentário